Coriolis, ou le mythe des lavabos
Qui n'a jamais entendu que les lavabos se vidaient dans un sens dans notre hémisphère, et dans l'autre sens dans l'autre ?
Nous allons nous pencher sur la question en termes simples, mais rappellons tout d'abord les résultats du sondage effectué :
32% des sondés soutiennent l'idée reçue
10% la démentent
58% ne se prononcent pas

Nous voilà partis dans une démonstration en deux parties : une première expliquant ce qu'est la force de Coriolis, une seconde s'intéressant à la mesure de cette force.
Qu'est-ce que la force de Coriolis ?
Préambule
Nous allons réduire la Terre pour cette démonstration à un manège tournant, dont le plan est perpendiculaire à l'axe de rotation de celle-ci.
Nous allons donc considérer que se déplacer de l'équateur vers un pôle revient à se rapprocher du centre du « manège ».
Enfin il faut connaître le sens de rotation de la Terre : Si on la regarde avec l'hémisphère Nord en haut, elle tourne de la gauche vers la droite (Dans le sens anti-horaire).
Étude du cas d'un manège
Voici une représentation d'un manège tournant :

La flèche noire représente le sens de rotation du manège. Les flèches rouges et bleues représentent les vitesses de deux points situés sur le manège : A et B.
Prenons une personne allant du centre du manège à sa périphérie :

Elle démarre avec une petite vitesse latérale (flèche bleue).
Un pas après, elle se retrouve sur un point possédant une plus grande vitesse latérale (flèche rouge).
Sa petite vitesse ne lui permet pas d'aller aussi vite que le manège, on a donc l'impression qu'elle est « déviée » dans le sens inverse de la marche (flèche verte).
Une animation explique simplement cet effet :
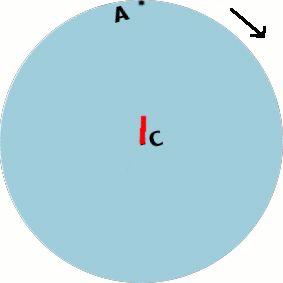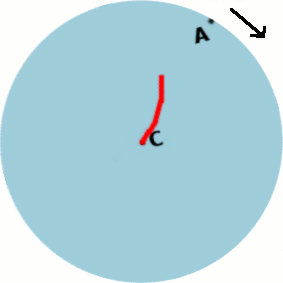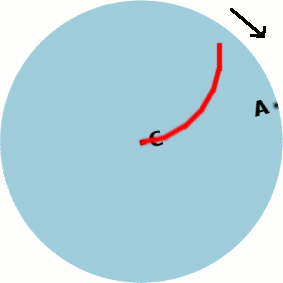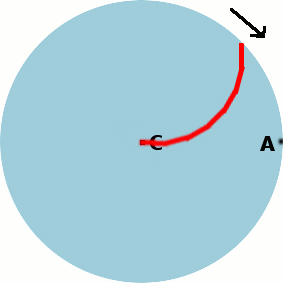
A chaque étape on s'avance vers le haut de l'image, mais entre-temps le manège bouge et on se retrouve "dévié".
Étude de tous les cas possibles :
Grâce à cette animation, on peut facilement trouver les résultats suivants :
Si on lance une balle du pôle Nord à l'équateur, elle sera déviée vers l'Ouest.
Si on lance une balle du pôle Sud à l'équateur, elle sera déviée vers l'Ouest.
Si on lance une balle de l'équateur au pôle Nord, elle sera déviée vers l'Est.
Si on lance une balle de l'équateur au pôle Sud, elle sera déviée vers l'Est.
Donc en théorie...
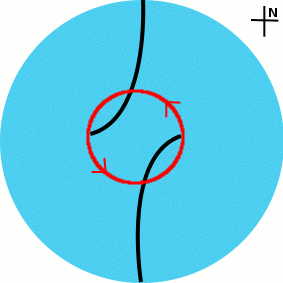
L'eau contenue dans le lavabo devrait tourner dans le sens anti-horaire.
Recherche de la démonstration
Cependant, pour observer cet effet, il faudrait que la différence de vitesse entre une particule se trouvant au bord du lavabo et une autre se trouvant au centre soit suffisante pour provoquer l'effet, et surtout, il faudrait que l'accélération de Coriolis ne soit pas « contrée » par des défauts dans le lavabo (frottements, différence de pente entre les parois, etc.).
Lorsque la Terre tourne sur elle-même, nous parcourons un petit cercle dont le rayon est égal au rayon de la Terre multiplié par le cosinus de la latitude.
Prenons l'exemple d'un lavabo de 40 cm de diamètre à 45° de latitude :
Calculons la vitesse du centre du lavabo :


Maintenant la vitesse du point du lavabo situé le plus au nord (20 cm plus haut) :
On cherche d'abord la variation en latitude (simple règle de trois) :

Donc la latitude du point du haut du lavabo est :
Et la différence de vitesse entre le bord et le centre du lavabo est :
Interprétation
Cela signifie qu'une goutte d'eau du centre du lavabo a une vitesse supérieure de 0,000 002 % à une goutte d'eau située au bord.
A titre de comparaison, pour un cyclone mesurant jusqu'à 5 km de rayon, la différence est de 0,05%.
On se rend bien compte que cette différence de vitesse ne permet en aucun cas de conclure que la force de Coriolis est suffisante pour dévier de manière visible de l'eau dans un lavabo.
Conclusion
Nous avons fait des expériences dans des bassines percées, avec des trous de différents diamètres : 6 mm, 8 mm, 10 mm. Nous nous sommes rendus compte que pour des trous de 6 et 8 mm, l'écoulement de l'eau était toujours radial. Pour un trou de 10 mm, nous avons observé des rotations de l'eau dans les deux sens, dans une proportion d'à peu près 50 %.
Nous concluons de ces recherches et de ces expériences que :
La force de Coriolis n'est pas assez forte pour dévier de l'eau dans un lavabo : on observe donc des écoulements radiaux dans la plupart des cas.
Alors pourquoi observe-t-on des rotations dans la bassine au trou de 10mm ?
Nous pensons que plus la vitesse d'écoulement est élevée, plus les chances de formation d'un tourbillon sont élevées : cela explique que pour un grand trou, donc une grande vitesse d'écoulement, se forment des tourbillons.
Pour télécharger le diaporama complet traitant de cette idée reçue, cliquez ici !
Vous pouvez télécharger Adobe Reader, le logiciel permettant de lire ce fichier, en cliquant sur le bouton ci-dessous :